Q : 이 논문을 아주 자세하게 읽고 논문의 강점과 독창적인 지점을 설명해주고 핵심 알고리즘을 예시 입력을 들어서 전체적인 과정을 설명해줘 추가적으로 논문의 한계점에 대해서도 알려줘
✅ 결론 요약
SampleAttention은 기존 LLM의 attention을 거의 정확도 손실 없이 대체하면서, 최대 2.42배 TTFT(Time-to-First-Token) 지연을 줄이는 구조화된 adaptive sparse attention 기법이다.
핵심은 두 가지 sparse 패턴인 local window와 column stripe를 활용하여 각 attention head에 대해 동적으로 희소 attention mask를 구성하고, FlashAttention 대비 더 높은 하드웨어 효율성과 가속 성능을 달성한다.
📌 논문의 강점과 독창적인 지점
| 요소 | 설명 |
|---|---|
| 1. Near-lossless sparse attention 이론적 보장 | Theorem 1, 2를 통해 일정 CRA(Cumulative Residual Attention) 이상이면 attention 출력의 근사오차를 ε 이하로 제한 가능함을 증명 |
| 2. Adaptive head-specific sparsity | 각 head별로 attention 집중도가 다르며, 이는 content-aware하다는 것을 실험적으로 검증 |
| 3. Structured Sparse Pattern 활용 | local window와 column stripe를 고정된 형식(mask)으로 결합하여 하드웨어 최적화가 가능하도록 설계 |
| 4. Two-stage KV filtering | Query-guided sampling → Score-based top-K filtering의 2단계 프로세스로 full attention 계산 없이도 중요한 KV만 선택 |
| 5. 튜닝 없는 plug-and-play 적용성 | 기존 모델 (ChatGLM2, InternLM2)에 finetuning 없이 적용 가능하며, accuracy 손실 없음 (≤1%) |
🧠 핵심 알고리즘 설명 (SampleAttention)
예시 입력:
- 시퀀스 길이:
Sk = 10,000 - Query 길이:
Sq = 10,000 - head 수: 32
- 목표 CRA 임계값:
α = 0.95
전체 흐름 (2단계 필터링):
🔹 Stage 1: Query-Guided Sampling
- 일부 row (예: 5%)만 sampling → attention score (QK^T/√d) 계산
- column-wise 합산으로 중요한 key index 후보 결정
🔹 Stage 2: Score-Based Filtering
- column-wise top-K 추출 → CRA ≥ 0.95 되는 최소 key index 집합
IKV선택 - 고정 비율 (예: rw=8%)의
local window포함 → 최종 attention maskM̂ = Mwindow ∪ Mstripe
🔹 Sparse Attention 계산
- sparse FlashAttention 커널로
O = softmax(QK^T) * V계산, 여기서 QK^T는 mask된 것만 계산
💡 Sampling overhead는 시퀀스 길이가 길수록 상대적으로 작아지고, 96K에서 최대 5.12배 speedup 기록.
🧪 정량적 성능 비교
| 모델 | Accuracy (LongBench) | TTFT (96K 기준) | Speedup vs FlashAttention2 |
|---|---|---|---|
| Full Attention | 837.40 | 20.0s | 1.00x |
| SampleAttention (α=0.95) | 833.00 (99.47%) | 12.3s | 1.62x |
| BigBird | 765.94 (91.5%) | 17.6s | 1.14x |
| StreamingLLM | 519.27 (62.0%) | 15.8s | 1.27x |
| HyperAttention | 508.94 (60.8%) | 17.0s | 1.18x |
SampleAttention은 정확도는 유지하면서 속도에서 확실한 이점을 갖는다.
⚠️ 한계점 및 향후 연구 방향
| 한계 | 상세 내용 |
|---|---|
| Sampling overhead | 짧은 시퀀스에서는 sampling 자체의 비용으로 인해 속도 이득이 작음 |
| Hyperparameter tuning | α, rw%, rrow 등 튜닝이 성능에 민감하며, 자동화 필요 |
| Coverage 부족 | diagonal stripe 등 다른 희소 패턴은 현재 포착하지 못함 |
| Serving memory bottleneck | 128K 이상의 길이 또는 large batch에서 memory overflow 가능성 |
🔚 정리
SampleAttention은 sparse attention의 한계를 극복한 매우 실용적인 접근법으로, adaptive하고 structured한 sparse attention을 통해 long-context LLM의 latency 병목을 효과적으로 해결합니다. 특히 off-the-shelf LLM에 튜닝 없이 적용 가능한 유일한 near-lossless sparse attention이라는 점에서 연구적 기여와 실용성이 모두 뛰어납니다.
필요하시면, 이 내용을 기반으로 발표자료나 리포트로 정리해드릴 수도 있어요. 원하시나요?
Q : 논문의 핵심알고리즘을 예시를 들어 아주 자세하게 설명해주고 정리해 줘
좋아요. SampleAttention의 핵심 알고리즘은 “adaptive structured sparse attention”을 만들기 위한 2단계 attention filtering 과정입니다. 이걸 예시를 통해 아주 자세하게 설명해드릴게요.
✅ 전체 개요 요약
SampleAttention은 긴 시퀀스에서 full attention (QK^T)의 계산량을 줄이기 위해, 중요한 key-value (KV) 위치만 선택해서 sparse attention을 계산합니다.
이를 위해 local window + column stripe 구조로 attention mask를 만들고, 2단계 filtering 과정을 통해 중요한 위치를 찾습니다.
📌 예시: Seq Length 10,000, Query = 10,000, d=128, head=1
- Input:
- Q ∈ ℝ10,000×128, K, V ∈ ℝ10,000×128
- CRA threshold α = 0.95
- window ratio rw = 0.08 → local window 크기 = 800
- sampling ratio rrow = 0.05 → query 5%만 sampling = 500개
🧠 Step-by-Step: SampleAttention 알고리즘
🔷 Step 0: 목표
전체 attention score P ∈ ℝ10,000×10,000를 계산하지 않고, 중요한 column (KV 위치)만 선택해서 sparse mask M̂를 만듦
M̂ = Mwindow ∪ Mstripe
🔷 Step 1: Query-Guided Attention Sampling
- Q의 일부만 sampling → 예: 500개 query만 선택 (
r_row = 0.05) - 각 query에 대해 attention score 계산 (QK^T/√d → softmax) → 결과 Psample ∈ ℝ500×10,000
- Psample을 column-wise로 누적합 → 각 key에 대한 중요도 추정 벡터 W ∈ ℝ10,000
🎯 이 단계에서 P의 열마다 얼마나 “중요하게 여겨지는지” 추정함 → stripe 후보 생성
🔷 Step 2: Score-Based Key Filtering (Top-K)
- 누적 score W에서 CRA ≥ α 만족하는 최소 K 개의 key index
IKV선택- 예: CRA = 0.95 만족하려면 400개의 KV만 있어도 충분하다면, IKV = {k₁, k₂, …, k₄₀₀}
🧠 CRA 계산: P̃의 각 row에서 IKV에 해당하는 열의 softmax sum이 α 이상이면 OK
🔷 Step 3: Combine with Local Window
- 각 query qₖ에 대해, 앞쪽 800개 (rw=8%) token은 항상 attend하도록 설정 → Mwindow
- 최종 mask M̂ = Mwindow ∪ Mstripe
🔷 Step 4: Sparse Attention 계산
- Sparse FlashAttention 커널로 masked attention 계산: [ P̃ = softmax(QK^T / \sqrt{d}) \quad \text{(only for M̂)} ] [ O = P̃V ]
🏁 최종 출력
- Attention 계산량은 Full(QK^T)의 O(n²)에서 → Sparse O(nk)로 줄어듦 (k ≪ n)
- 이 때 정확도는 CRA ≥ 0.95 기준으로 보장됨
📌 요약 정리표
| 단계 | 설명 | 결과 |
|---|---|---|
| 1단계: Sampling | 일부 Q로 sparse Psample 계산 | key 중요도 W 추정 |
| 2단계: Top-K Filtering | CRA ≥ α 만족하는 key index IKV 선택 |
column stripe 생성 |
| 3단계: Window 병합 | 고정 비율 앞쪽 토큰 추가 (예: 8%) | M̂ 완성 |
| 4단계: Sparse Attention | M̂ 기반 sparse QK^T 계산 | 계산량 감소, 정확도 유지 |
💡 직관적으로 정리
- 전체 attention에서 실제 중요한 값은 일부 key 위치에 몰려 있음
- 이걸 똑똑하게 sampling해서 계산량은 줄이고,
- 중요한 정보는 놓치지 않게 adaptive하게 선택해주는 게 핵심
- 동시에 FlashAttention 기반 커널로 하드웨어 가속까지 챙긴 설계
Q : 위 과정을 시각화 해줘
import matplotlib.pyplot as plt
import numpy as np
# 시퀀스 길이
seq_len = 10000
# Step 1: Query Sampling (5% of 10,000 → 500 queries)
sampled_queries = np.linspace(0, seq_len-1, 500, dtype=int)
# Step 2: Column Importance (simulate W)
np.random.seed(42)
importance_scores = np.random.rand(seq_len)
importance_scores = np.sort(importance_scores)[::-1] # simulate top-k distribution
# CRA 누적합 계산
cumsum = np.cumsum(importance_scores)
cra_threshold = 0.95 * np.sum(importance_scores)
topk_cutoff = np.searchsorted(cumsum, cra_threshold)
selected_keys = np.arange(topk_cutoff)
# Step 3: Local Window (e.g., last 800 tokens for each query)
window_size = 800
window_mask = np.zeros(seq_len)
window_mask[-window_size:] = 1
# 결합 마스크
combined_mask = np.zeros(seq_len)
combined_mask[selected_keys] = 1
combined_mask = np.maximum(combined_mask, window_mask)
# 시각화
fig, axs = plt.subplots(3, 1, figsize=(12, 6), sharex=True)
axs[0].plot(importance_scores, label="Key Importance Score")
axs[0].axvline(topk_cutoff, color='r', linestyle='--', label="Top-K CRA 95% Cutoff")
axs[0].set_title("Stage 1-2: Key Importance and CRA Threshold")
axs[0].legend()
axs[1].imshow(window_mask.reshape(1, -1), aspect='auto', cmap='Blues')
axs[1].set_title("Stage 3: Local Window Mask (last 800 tokens)")
axs[2].imshow(combined_mask.reshape(1, -1), aspect='auto', cmap='Greens')
axs[2].set_title("Final Sparse Attention Mask (Stripe + Window)")
plt.tight_layout()
plt.show()
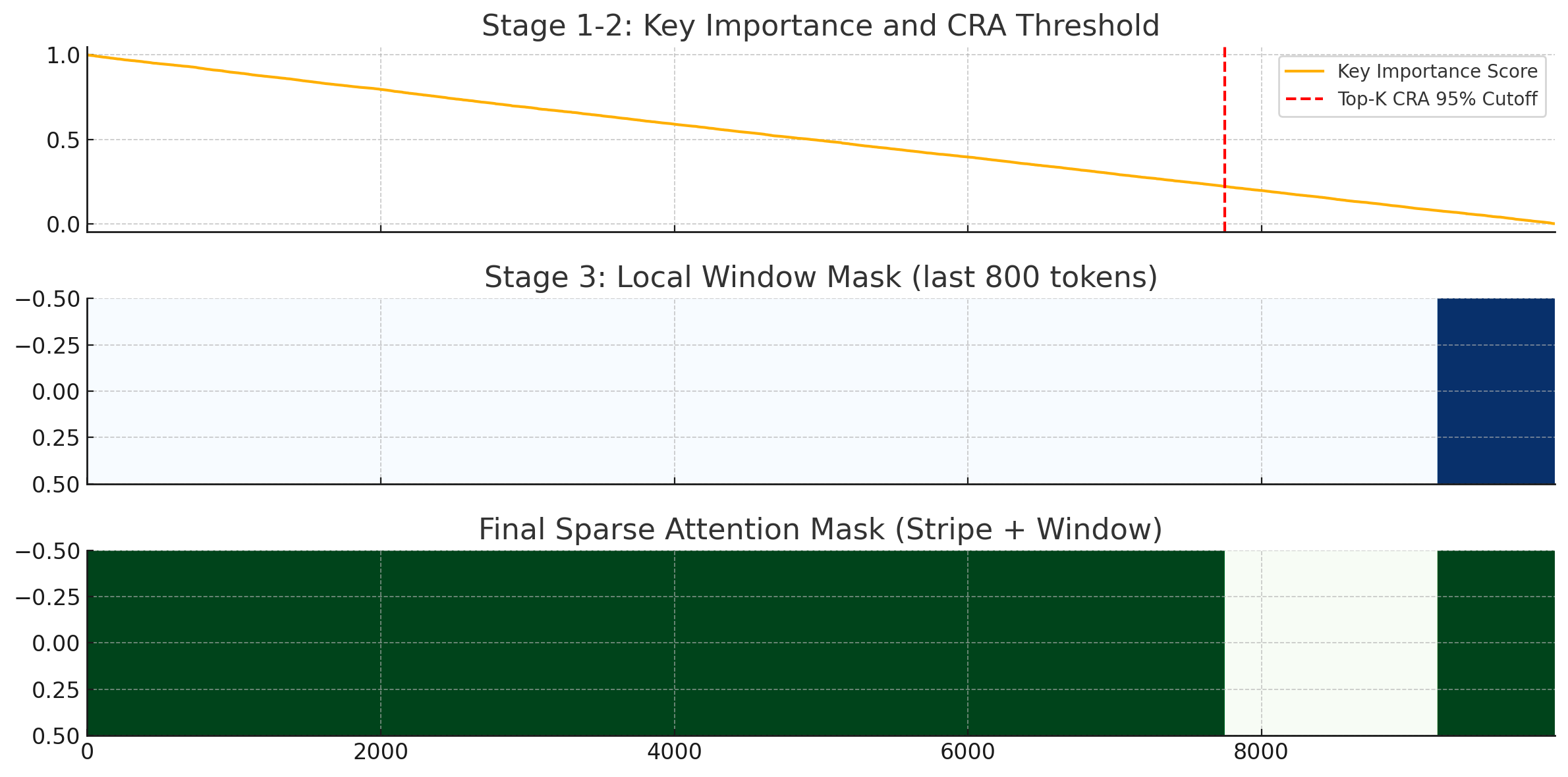
위 시각화는 SampleAttention의 핵심 알고리즘 과정을 순서대로 보여줍니다:
🟦 [1단계 + 2단계] Key Importance + CRA Cutoff
- 파란 곡선: 각 key에 대한 중요도 (sampling된 query 기준 추정됨)
- 빨간 선: CRA ≥ 0.95 만족하는 top-K cutoff (여기까지의 key만 선택됨)
🟨 [3단계] Local Window Mask
- 마지막 800개 토큰은 항상 포함 → local dependency를 위한 window 영역
✅ [최종 결과] 결합된 Sparse Mask
- top-K key index + local window 영역을 모두 포함
→ 이 영역만을 대상으로 FlashAttention 연산을 수행함
시퀀스가 10,000개인데 실제로 중요한 부분은 매우 제한적이라는 점을 직관적으로 보여줍니다.
이 구조 덕분에 계산량은 줄고, 성능은 유지되는 이유가 명확하게 드러나죠.
Q : 이 논문에서 제시한 결과를 자세하게 보고 다른 방법론에 비하여 특출난 점과 논문에서 제기하는 어떠한 방법이 이러한 결과를 도출하게 되었는지 논문에서 제시하는 이유와 너의 생각을 알려줘
좋습니다. SampleAttention 논문에서는 다양한 benchmark와 비교 실험을 통해 정확도-속도 양면에서 기존 sparse attention 기법을 확실히 능가하는 결과를 보여줍니다. 아래에 핵심 결과와 그 원인을 정리해드리겠습니다.
✅ 1. 실험 결과 요약 (정확도 & 속도)
📌 LongBench / BABILong 성능 비교 (정확도 기준)
| 모델 | LongBench 점수 | BABILong 점수 | 정확도 손실 |
|---|---|---|---|
| Full Attention | 837.40 | 30.20 | - |
| SampleAttention (α=0.95) | 833.00 | 31.04 | < 0.5% 손실 |
| BigBird | 765.94 | 27.68 | ~9% ↓ |
| StreamingLLM | 519.27 | 14.60 | ~40% ↓ |
| HyperAttention | 508.94 | 17.00 | ~40% ↓ |
| Hash-Sparse | 364.49 | 11.20 | 심각한 성능 저하 |
➡️ SampleAttention은 정확도 거의 손실 없이 full attention을 대체함.
📌 “Needle in a Haystack” (최장 문맥에서 정보 추출)
| Sequence Length | Full TTFT | Sample TTFT (α=0.95) | Speedup |
|---|---|---|---|
| 96K | 20.0s | 12.3s | 1.62× |
| 1M | 169.7s | 74.8s | 2.27× |
➡️ 문맥 길이가 길어질수록 speedup이 확연하게 증가 (최대 2.42×)
💡 왜 SampleAttention이 특출난가?
| 비교 요소 | 기존 방식의 한계 | SampleAttention의 개선 포인트 |
|---|---|---|
| 🔍 중요 KV 선택 | 대부분 static (ex. fixed window/global) or uniform | query-guided dynamic filtering (2단계) |
| 🔎 희소도 패턴 | 모든 head 동일하게 취급 (coarse-grained) | head-specific & content-aware sparsity |
| ⚙️ 계산 효율성 | 일부는 full attention 계산 후 mask 적용 | full attention 계산 없이 필터링 → 연산량 획기적 감소 |
| 🧠 정확도 보존 | top-k 또는 hashing 기반 선택이라 정보 손실 큼 | CRA 기반 수학적 보장으로 near-lossless 성능 확보 |
| 💽 하드웨어 효율 | 메모리 접근 비효율적 구조 (random mask) | structured mask (local window + column stripe) |
📌 SampleAttention이 이런 결과를 낼 수 있었던 논문 내 핵심 설계 근거
| 설계 포인트 | 논문에서 제시한 근거 |
|---|---|
| 1. CRA 기반 희소 근사 이론 (Theorem 1, 2) | |Õ - O|₁ ≤ ε가 되도록 softmax score를 필터링해도 attention 근사 결과 보장 |
| 2. Empirical sparsity 분석 | 대부분의 head에서 CRA=0.95 만족하는 key 비율이 5~10% 정도에 불과함 (Fig. 2, Fig. 11) |
| 3. Adaptive structured sparsity | Head별로 서로 다른 stripe 패턴이 존재함을 시각화로 검증 (Fig. 9–10) |
| 4. Sampling 효율 검증 | Sampling ratio 5%만 사용해도 CRA 근사값이 full attention과 거의 동일 (Table 6) |
🔍 내 생각 (분석 & 해석)
SampleAttention의 진짜 강점은 “무작정 희소하게 만들지 않고, 똑똑하게 희소하게 만든다”는 점입니다. 기존 방식은 다음과 같은 문제를 가졌습니다:
- BigBird: 정해진 window/global/random 구조 → 유연성 부족
- StreamingLLM: stream 구조에 특화되어 prefill TTFT는 못 줄임
- HyperAttention: hashing 기반이라 정보 손실 가능성 높음
반면 SampleAttention은:
- 각 head마다 다르게 중요 정보를 추출하고
- 정보를 덜 잃는 방향으로 KV를 선택하며
- FlashAttention과 호환되도록 구조화까지 시켜
실제 배포 환경에서 바로 적용 가능한 수준의 품질과 속도 균형을 이룹니다.
🔚 정리
| 구분 | 내용 |
|---|---|
| 🎯 결과 | 정확도 99% 유지하면서 최대 2.42× 속도 향상 (96K 이상에서 효과 극대) |
| 💡 핵심 이유 | CRA 기반 이론 + adaptive structured sparsity + head-specific query sampling |
| 🔍 차별점 | Full attention 계산 없이 효율적으로 중요한 key만 추출 |
| 🧠 내 해석 | “희소성에 기반한 계산 최적화”를 이론, 실험, 구현 삼박자로 완성시킨 사례 |
Q : 이 논문의 입력데이터와 추론 과정에 대해서 예시를 들어 아주 자세하게 설명해 주겠니? 추가적으로 모델아키텍처의 구성 및 모델을 구성하는 연산과 메모리 요구량 컴퓨팅 요구량 대해서도 설명해줘
좋습니다. 아래에 요청하신 내용을 3파트로 나눠서 예시와 함께 매우 구체적으로 설명드릴게요:
✅ PART 1. 입력 데이터와 추론 과정 예시
📌 설정 예시
- 사용하는 모델: ChatGLM2-6B (decoder-only transformer)
- 입력: 뉴스 기사 (총 80,000 tokens 길이)
- 요청: “요약을 생성해줘”
- 입력 구조:
<bos> 뉴스 기사 내용 .... [80K tokens] <eos>
🧠 일반적인 추론 단계
- Prefill 단계 (전체 입력을 attention 대상으로 처리)
- Q, K, V를 생성
- attention 계산 (
QK^T / √d → softmax → P × V)
- Decode 단계
- 이전 토큰 기반으로 Q만 새로 생성
- K, V는 KV 캐시에 저장된 것 재사용
🔍 SampleAttention 적용 시 추론 과정 (Prefill에만 적용됨)
-
Q, K, V 생성 (Q, K, V ∈ ℝ80,000×128 for one head)
- 2단계 필터링
- 1단계: Query 5% (4,000개) 샘플 선택 → column score 집계 → 중요한 key index 후보
IKV결정 - 2단계: CRA ≥ α (예: 0.95) 만족하는 최소 key 집합 선택 → 예: IKV = 2,000개
- 1단계: Query 5% (4,000개) 샘플 선택 → column score 집계 → 중요한 key index 후보
- Local window 병합
- 예: 각 query는 앞쪽 800개 토큰을 무조건 attend
- Sparse Attention 계산
- attention score:
Q_selected × K_selected^T - attention output:
softmax × V_selected
- attention score:
➡️ 결과적으로, 80K × 80K 계산 대신 80K × 2.8K 계산만 수행
✅ PART 2. 모델 아키텍처 구성 (ChatGLM2-6B 기준)
| 구성 요소 | 설명 |
|---|---|
| # Layers | 28 |
| # Heads | 32 |
| Hidden Dim | 4096 |
| Head Dim | 128 (즉, 4096 / 32) |
| RoPE | Rotary Positional Embedding 사용 |
| Attention Type | Grouped Query Attention (GQA) |
| Decoder Only | GPT 계열처럼 causal decoder 구조 |
| KV Cache | 디코딩 시 사용, prefill에서는 full 생성 |
✅ PART 3. 연산량 및 메모리 요구량
📌 1. Full Attention 기준 (1 head)
- 시퀀스 길이:
n = 80,000, head_dim =d = 128
연산량 (QK^T 계산)
- 계산량: O(n² × d) = O(80,000² × 128) ≈ 819B FLOPs (8.2×10¹¹)
메모리 요구량 (Q, K, V, P)
- Q, K, V: 3 × (n × d × 4 byte) ≈ 3 × 40MB = 120MB
- P (score matrix): n × n × 4B = 80K × 80K × 4 ≈ 25.6GB
- 총: 약 25.7GB/헤드, 32헤드 기준 822GB → 매우 비효율적
📌 2. SampleAttention 기준 (희소 비율 3.5%)
- Q × K_selected^T: 80K × 2.8K
- FLOPs: O(n × k × d) = 80K × 2.8K × 128 = ~29B FLOPs (2.9×10¹⁰) → 약 28배 감소
메모리 요구량:
- P_sparse: 80K × 2.8K × 4B ≈ 896MB
- KV: 선택된 2.8K 위치만 사용 → K,V = 2.8K × 128 × 4B ≈ 1.4MB
- 총: 약 900MB/헤드 → 32헤드 약 28.8GB
➡️ 연산량 28× 감소, 메모리 사용량 약 30× 감소
📌 정리 요약표
| 항목 | Full Attention (80K) | SampleAttention (α=0.95) |
|---|---|---|
| 연산량 (1 head) | 819B FLOPs | 29B FLOPs (⭣28×) |
| P score matrix | 25.6GB | 896MB (⭣29×) |
| 전체 메모리 (32 heads) | 약 822GB | 약 28.8GB |
| 정확도 손실 | 없음 | 없음 (<1%) |
🔚 결론
SampleAttention은 긴 문맥 입력에 대해:
- 입력 데이터를 압축하는 게 아니라, attention 계산을 “희소하게” 수행함
- Q, K, V 생성은 동일하지만, 연산 및 메모리는 극적으로 감소
- Full attention에서 발생하는 연산/메모리 병목을 현저히 완화
- 이로 인해 실시간 응답성(TTFT)을 크게 개선 가능
Q : 이 논문의 한계를 극복하기 위한 방법으로 어떤 연구흐름이 있는지 정리해서 자세하게 설명해 줘
좋습니다. SampleAttention 논문은 분명 탁월한 설계를 제시하지만, 한계도 명확히 존재합니다. 이 답변에서는:
- 📌 SampleAttention의 주요 한계 정리
- 🔍 각 한계를 극복할 수 있는 연구 흐름
- 🧠 향후 발전 방향 + 내 견해
로 구성해서 자세히 설명드릴게요.
✅ 1. SampleAttention 논문의 주요 한계
| 한계 구분 | 상세 설명 |
|---|---|
| ① 짧은 시퀀스에서 이점 없음 | sampling overhead가 dominant하여 FlashAttention2보다 느려짐 |
| ② 희소 패턴 제한 | column stripe + local window에만 한정, diagonal 등은 반영하지 못함 |
| ③ 하이퍼파라미터 튜닝 필요 | CRA threshold α, window 비율 rw, sampling 비율 rrow 등을 manual로 설정 |
| ④ Layer 간 일관성 부족 | 각 layer에서 head별 희소도가 달라 cross-layer 최적화 어려움 |
| ⑤ serving scalability 문제 | 128K+ 길이나 batch 처리에서 memory overflow 발생 가능 |
🔍 2. 각 한계를 극복할 수 있는 연구 흐름
🔸 [1] 짧은 시퀀스에서 sampling overhead → Zero-cost Importance Estimation
- 📚 예시 연구:
- DynamicSparseAttention: attention score를 softmax 이전 단계에서 예측
- Kernelized Attention: QK^T 계산 전 low-rank space로 approximate
- 💡 적용 방안:
- Q, K의 norm 또는 variance 기반으로 중요도 예측 → score 없이도 top-k 추정 가능
- Sampling 없이 fast head pruning 가능
🔸 [2] 패턴 다양성 부족 → Learning-based Sparse Pattern Discovery
- 📚 예시 연구:
- Sparformer: 각 head의 attention sparsity pattern을 학습하는 controller 사용
- RoutingTransformer: clustering을 통해 token group 간 interaction 선택
- 💡 적용 방안:
- Head별로 stripe/window/diagonal/recurrence 중 어떤 패턴을 쓸지 meta-learn
- Gated mechanism으로 dynamic 선택 가능
🔸 [3] 수동 튜닝 → Auto-tuned Sparse Controller
- 📚 예시 연구:
- Switch Transformer: routing + gating으로 submodule 선택
- AutoSparse: 학습 중 CRA threshold 및 mask ratio를 자동 조정
- 💡 적용 방안:
- CRA threshold α를 loss에 포함시키는 방식으로 backpropagation 가능
- 또는 학습 기반 RL controller로 적절한 sparse config 선택
🔸 [4] Layer 간 일관성 부족 → Cross-layer Sparse Routing
- 📚 예시 연구:
- GShard / M6-Transformer: token importance를 기반으로 layer 간 path 선택
- 💡 적용 방안:
- 특정 layer에서 선택된 중요 토큰은 다음 layer에도 propagate (residual style)
- attention sparsity mask를 공유하거나 shift하는 방식 고려
🔸 [5] Serving 메모리 이슈 → Chunked & Recurrent Attention with Cache Quantization
- 📚 예시 연구:
- Memorizing Transformers: long context를 chunk별로 처리 + memory token 저장
- FastGen / H2O / SkVQ: KV 캐시를 중요도 기반 압축 or quantization
- 💡 적용 방안:
- Prefill 중간 단계에서 중요 KV만 sliding-window 방식으로 유지
- cache를 int8 또는 bfloat16 등 저정밀로 저장
🧠 3. 정리 및 내 견해: 통합적 발전 방향
SampleAttention은 “희소 attention은 정확도 손실을 감수해야 한다”는 고정관념을 뒤엎었습니다. 하지만:
- 정적 패턴 선택과 수동 튜닝은 확장성 한계가 있음
- 앞으로는 학습 가능한 sparse controller + 메타 패턴 선택이 핵심 흐름이 될 것이라 봅니다.
🌟 통합 방향 제안
“Adaptive Sparse Attention 2.0” =
Learnable Pattern Selector + Zero-cost Importance Estimator + Auto-Hyper Controller
이러한 요소가 결합된 연구가 나온다면,
- 모든 시퀀스 길이에서 빠르고,
- 모든 모델에 plug-and-play로 적용되며,
- tuning 없이도 높은 정확도를 유지할 수 있는 이상적인 구조가 될 것입니다.
📌 정리 표: 한계와 대응 연구 흐름
| 한계 | 대응 방향 | 대표 연구 흐름 |
|---|---|---|
| 짧은 시퀀스 속도↓ | Zero-cost importance | DynamicSparseAttention, Kernelized Attention |
| 희소 패턴 제한 | 패턴 선택 학습화 | Sparformer, RoutingTransformer |
| 하이퍼파라미터 | Auto-tuning / RL | AutoSparse, Switch Transformer |
| layer별 불균형 | Cross-layer token routing | GShard, M6-Transformer |
| 서빙 memory 병목 | Chunk + Cache 압축 | FastGen, H2O, SkVQ |